avl树

定义

在一个二叉搜索树中，每个结点的左右子树的高度差绝对值小于等于1的二叉搜索树，被称为平衡二叉树。avl树是最早出现的平衡二叉树。

优势

avl树的查找、插入、删除的时间复杂度都是O(logN)

平衡因子

平衡因子是左子树的高度减去右子树的高度所得结果，记为bf,bf的合法范围为-1,0,1。某个结点的平衡因子超出这个范围，那么这个结点就是不平衡的。需要做旋转处理。当bf的值为-2或2时，即左子树的高度比右子树的高度小2或左子树的高度比右子树的高度大2，做树旋转。

树旋转

左左旋转

如果插入的新结点是当前结点的左子树的左孩子,做一次右旋转即可平衡，称为左左旋转

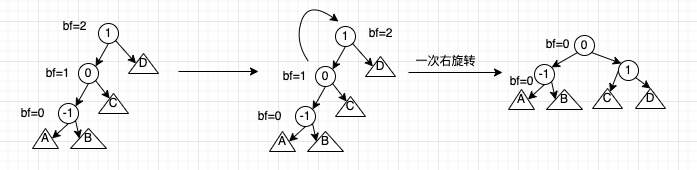
右右旋转

如果插入的新结点是当前结点右子树的右孩子，做一次左旋转即可平衡，称为右右旋转

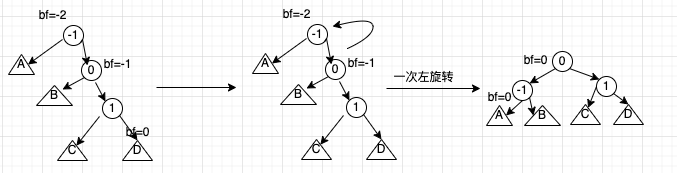
左右旋转

如果插入的新结点是当前结点左子树的右孩子，需要做两次旋转，先做一次左旋转，再做一次右旋转，称为左右旋转

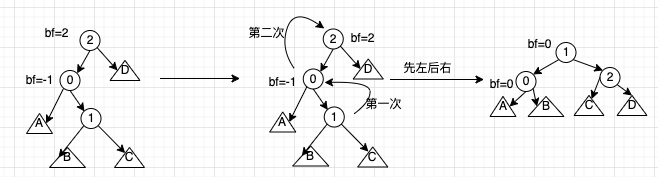
右左旋转

如果插入的新结点是当前结点右子树的左孩子，也需要做两次旋转，先做一次右旋转，再做一次左旋转，称为右左旋转

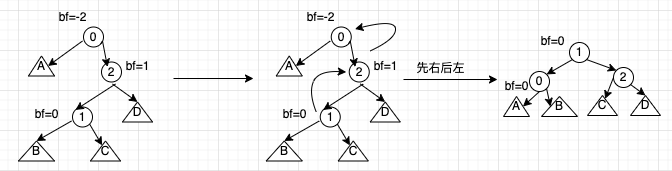
插入

按照普通的搜索二叉树来插入，然后判断树是否平衡，如果不平衡，则做树旋转，使之重新平衡。

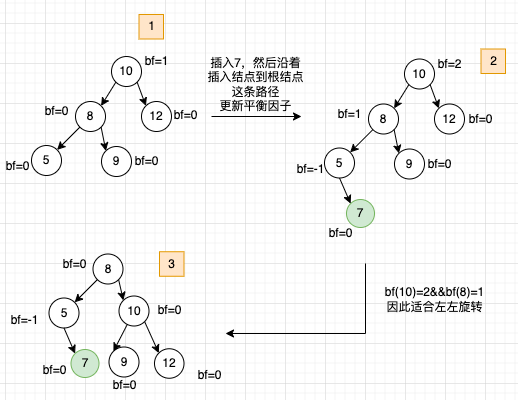
第一步，按照普通二叉搜索树的插入算法来插入新结点，上图插入结点7
第二步，沿着结点7到根结点这条路径更新平衡因子如果某个结点的平衡因子超出[-1,0,1]范围，这个结点需要处理
第三步，按照以下情形来做树旋转，上图适合左左旋转

1. 如果BF(node) = 2 and BF(node -> left-child) = 1, 做左左旋转
2. 如果BF(node) = -2 and BF(node -> right-child) = -1, 做右右旋转
3. 如果BF(node) = 2 and BF(node -> left-child) = -1, 做左右旋转
4. 如果BF(node) = -2 and BF(node -> right-child) = 1, 做右左旋转

删除

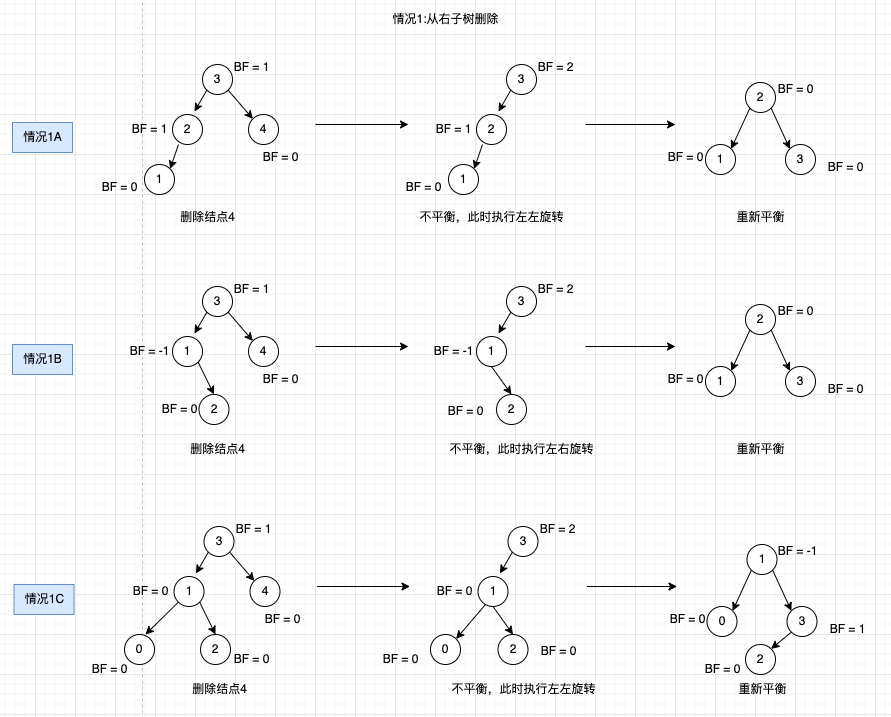
删除操作和插入操作一样，也是按照搜索二叉树的删除算法来删除，然后判断是否需要做平衡处理。如有需要，则执行树旋转。
有两种情况：
情况1，从右子树删除，使得右子树高度减一。

• 1A. 如果 BF(node) = +2 and BF(node -> left-child) = +1, 执行左左旋转.
• 1B. 如果 BF(node) = +2 and BF(node -> left-child) = -1, 执行左右旋转.
• 1C. 如果 BF(node) = +2 and BF(node -> left-child) = 0, 执行左左旋转.

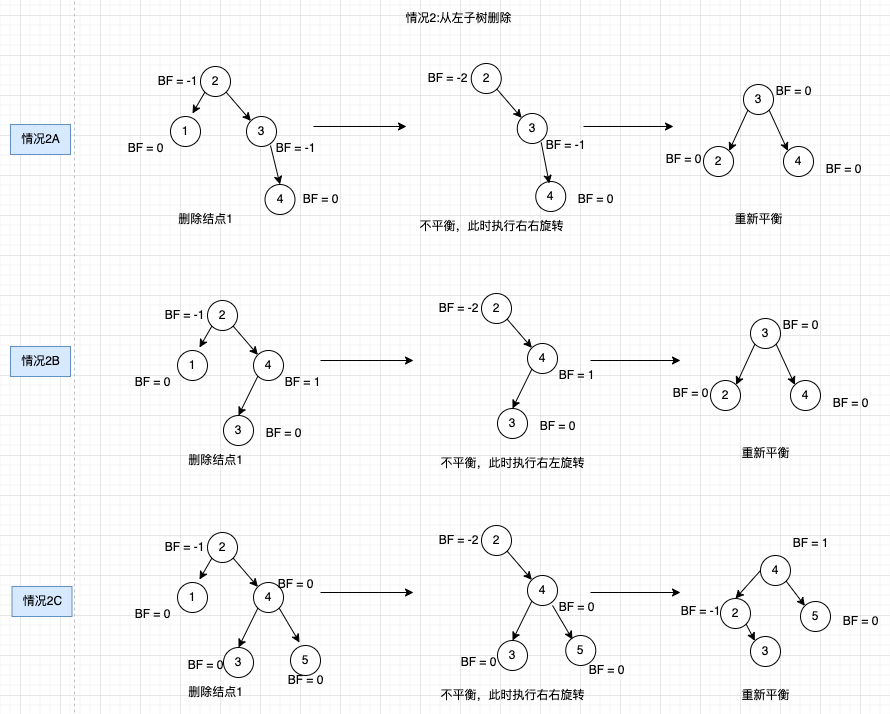
情况2，从左子树删除，使得左子树高度减一。

• 2A. 如果 BF(node) = -2 and BF(node -> right-child) = -1, 执行右右旋转.
• 2B. 如果 BF(node) = -2 and BF(node -> right-child) = +1, 执行右左旋转.
• 2C. 如果 BF(node) = -2 and BF(node -> right-child) = 0, 执行右右旋转.

代码

using namespace std;

struct node {
    struct node *left;
    int data;
    int height;
    struct node *right;
};

class AVL
{
private:
    
public:
    struct node * root;
    AVL(){
        this->root = NULL;
        
    }
    
    int calheight(struct node *p){
        
        if(p->left && p->right){
            if (p->left->height < p->right->height)
                return p->right->height + 1;
            else return  p->left->height + 1;
        }
        else if(p->left && p->right == NULL){
            return p->left->height + 1;
        }
        else if(p->left ==NULL && p->right){
            return p->right->height + 1;
        }
        return 0;
    }
    
    int bf(struct node *n){
        if(n->left && n->right){
            return n->left->height - n->right->height;
        }
        else if(n->left && n->right == NULL){
            return n->left->height;
        }
        else if(n->left== NULL && n->right ){
            return -n->right->height;
        }
        return 0;
    }
    
    struct node * llrotation(struct node *n){
        struct node *p;
        struct node *tp;
        p = n;
        tp = p->left;
        
        p->left = tp->right;
        tp->right = p;
        
        return tp;
    }
    
    
    struct node * rrrotation(struct node *n){
        struct node *p;
        struct node *tp;
        p = n;
        tp = p->right;
        
        p->right = tp->left;
        tp->left = p;
        
        return tp;
    }
    
    
    struct node * rlrotation(struct node *n){
        struct node *p;
        struct node *tp;
        struct node *tp2;
        p = n;
        tp = p->right;
        tp2 =p->right->left;
        
        p -> right = tp2->left;
        tp ->left = tp2->right;
        tp2 ->left = p;
        tp2->right = tp;
        
        return tp2;
    }
    
    struct node * lrrotation(struct node *n){
        struct node *p;
        struct node *tp;
        struct node *tp2;
        p = n;
        tp = p->left;
        tp2 =p->left->right;
        
        p -> left = tp2->right;
        tp ->right = tp2->left;
        tp2 ->right = p;
        tp2->left = tp;
        
        return tp2;
    }
    
    struct node* insert(struct node *r,int data){
        
        if(r==NULL){
            struct node *n;
            n = new struct node;
            n->data = data;
            r = n;
            r->left = r->right = NULL;
            r->height = 1;
            return r;
        }
        else{
            if(data < r->data)
                r->left = insert(r->left,data);
            else
                r->right = insert(r->right,data);
        }
        
        r->height = calheight(r);
        
        if(bf(r)==2 && bf(r->left)==1){
            r = llrotation(r);
        }
        else if(bf(r)==-2 && bf(r->right)==-1){
            r = rrrotation(r);
        }
        else if(bf(r)==-2 && bf(r->right)==1){
            r = rlrotation(r);
        }
        else if(bf(r)==2 && bf(r->left)==-1){
            r = lrrotation(r);
        }
        
        return r;
        
    }
    
    struct node * deleteNode(struct node *p,int data){
        
        if(p->left == NULL && p->right == NULL){
            if(p==this->root)
                this->root = NULL;
            delete p;
            return NULL;
        }
        
        struct node *t;
        struct node *q;
        if(p->data < data){
            p->right = deleteNode(p->right,data);
        }
        else if(p->data > data){
            p->left = deleteNode(p->left,data);
        }
        else{
            if(p->left != NULL){
                q = inpre(p->left);
                p->data = q->data;
                p->left=deleteNode(p->left,q->data);
            }
            else{
                q = insuc(p->right);
                p->data = q->data;
                p->right = deleteNode(p->right,q->data);
            }
        }
        
        if(bf(p)==2 && bf(p->left)==1){ p = llrotation(p); }
        else if(bf(p)==2 && bf(p->left)==-1){ p = lrrotation(p); }
        else if(bf(p)==2 && bf(p->left)==0){ p = llrotation(p); }
        else if(bf(p)==-2 && bf(p->right)==-1){ p = rrrotation(p); }
        else if(bf(p)==-2 && bf(p->right)==1){ p = rlrotation(p); }
        else if(bf(p)==-2 && bf(p->right)==0){ p = llrotation(p); }
        
        
        return p;
    }
    
    struct node* inpre(struct node* p){
        while(p->right!=NULL)
            p = p->right;
        return p;
    }
    
    struct node* insuc(struct node* p){
        while(p->left!=NULL)
            p = p->left;
        
        return p;
    }
    
    ~AVL(){
        
    }
};